Come interpretare i grafici HLog e QLN
Sulle linee VDSL uno degli strumenti più utili per valutare la qualità della linea sono i grafici HLog e QLN, che rappresentano rispettivamente l’attenuazione della linea in base alla frequenza e il rumore di fondo.
Questo articolo spiega come interpretare questi due grafici, provando ad usare un linguaggio alla portata di tutti. Per questo motivo i concetti esposti sono notevolmente semplificati e potrebbero apparire come imprecisi ai più esperti.
Il grafico HLog
Partiamo dal grafico in sé e per sé:
sull’asse delle ascisse (le
x) sono indicate alternativamente le frequenze o le portanti. Le frequenze più comuni in VDSL2 sono:- Profilo 17a: 17,664 MHz (4096 portanti)
- Profilo 35b: 35,328 MHz (8192 portanti)
sull’asse delle ordinate (le
y) è indicata l’attenuazione del cavo espressa in decibel (dB). In FTTC il valore massimo per cui si può utilizzare una portante per allocare bit è approssimabile a circa -60 dB.
In altre parole, il grafico HLog rappresenta l’attenuazione del cavo alle diverse frequenze utilizzate.
Quali informazioni può fornire un HLog
Da un HLog è possibile:
- stimare la lunghezza della tratta in rame;
- osservare la presenza alcuni problemi sulla coppia;
- verificare se la linea ha un falso contatto (“viaggia su un filo solo”);
- osservare la presenza di derivazioni (stub) e calcolarne la lunghezza.
In seguito sono analizzati i casi singolarmente.
Stimare la lunghezza della linea
La lunghezza della tratta viene calcolata considerando il kl0 della linea, ossia l’attenuazione a 1 MHz (portante 232).
Di seguito è riportata una tabella con alcuni valori di kl0 per alcuni cavi Telecom Italia, per farsi un’idea.
| Cavo | Attenuazione a 1 MHz / 1000 metri |
|---|---|
| TI 1240 0,4 mm | <= 27 dB |
| TI 1240 0,6 mm | <= 19 dB |
| CT 948 0,75 mm (alluminio) | <= 19 dB |
Possibili problemi sulla coppia
Un HLog ideale dovrebbe essere, volendo utilizzare un linguaggio rigoroso, monotono decrescente, ossia simile a questo grafico:
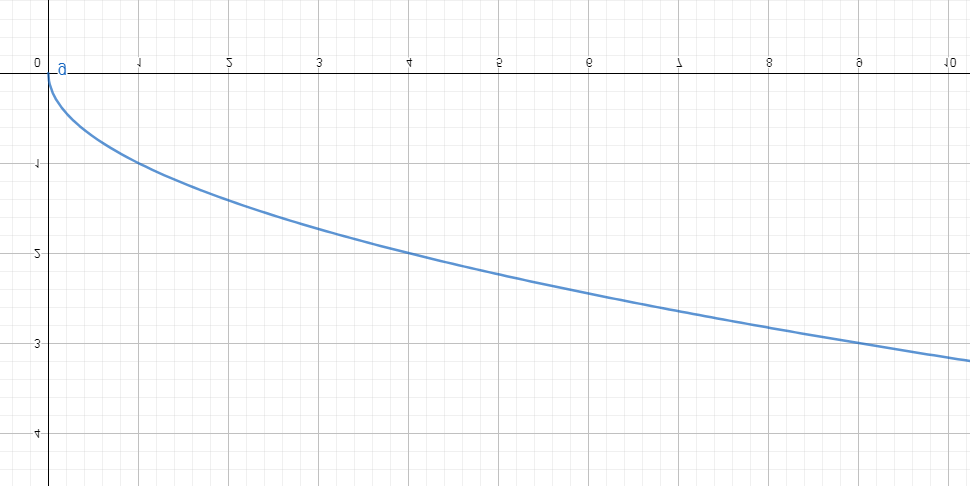
In altre parole, significa che ogni punto del grafico dovrebbe avere un valore più “alto” del punto successivo. (Ci perdonino i matematici.)
In un caso reale, un “buon” HLog si presenta così:
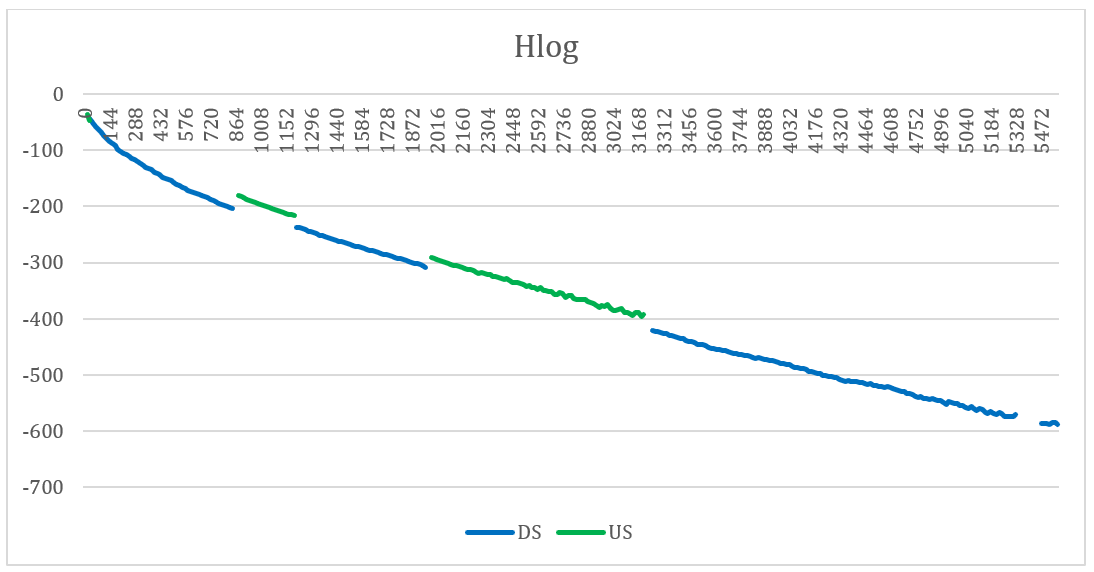
Tuttavia nella realtà è normale avere una leggera oscillazione dei valori. Per esempio, si consideri il seguente grafico:
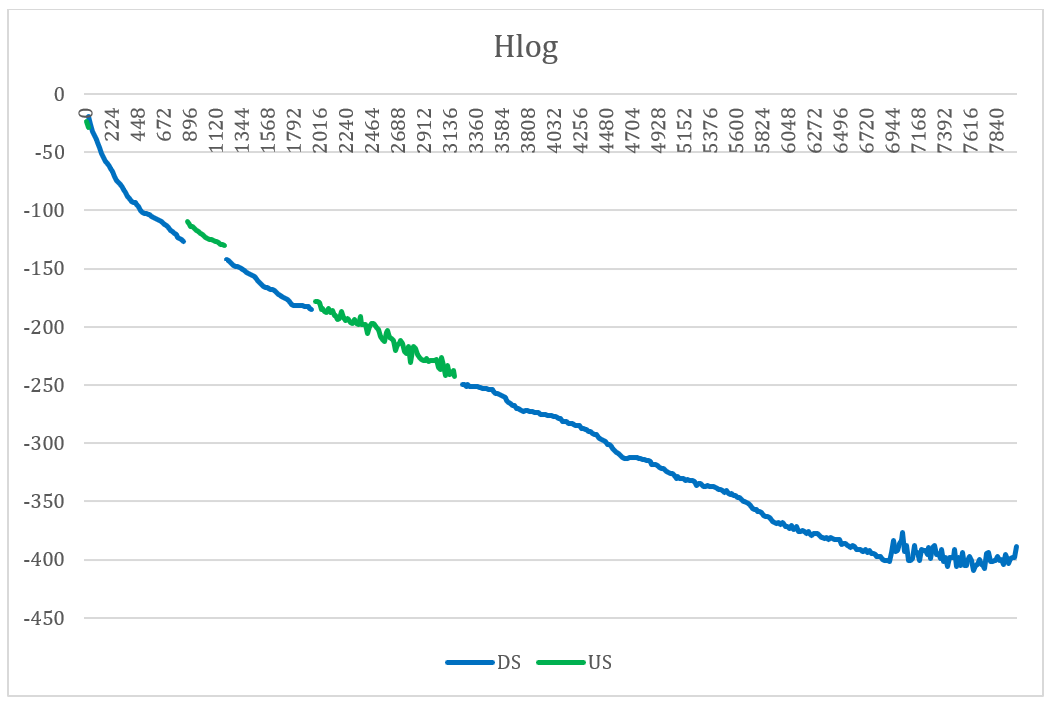
Si può notare una oscillazione (come fosse il grafico di un sismografo) sulla terza tratta verde (US2 e US3) e sul finale della tratta blu (DS3).
Idealmente tali oscillazioni non dovrebbero esserci, ma può capitare di vederle. Se l’impianto di casa è già stato sistemato (vedi guida al sezionamento), indicativamente non bisogna pensarci troppo fintanto che l’ampiezza delle oscillazioni (“quanto sono alte”) non supera i 7/8 dB.
Una grossa oscillazione (superiore a ±10 dB) invece può essere sintomo di problemi sulla coppia.
Verificare se la linea ha un falso contatto
Un falso contatto comporta un effetto capacitivo a uno dei due capi dei conduttori, che si manifesta sul grafico come un aumento delle attenuazioni alle frequenze più basse.
Pertanto, un falso contatto sarà rilevabile osservando la US0 e la DS1: a differenza di un un HLog normale, la curva nella parte iniziale non “punterà” in basso a destra ma in alto a destra, ovvero, in termini più rigorosi, la curva diventerà (su un certo intervallo) monotona crescente.
Prendendo come riferimento il grafico ideale mostrato sopra, una versione in cui è presente un falso contatto apparirebbe così:
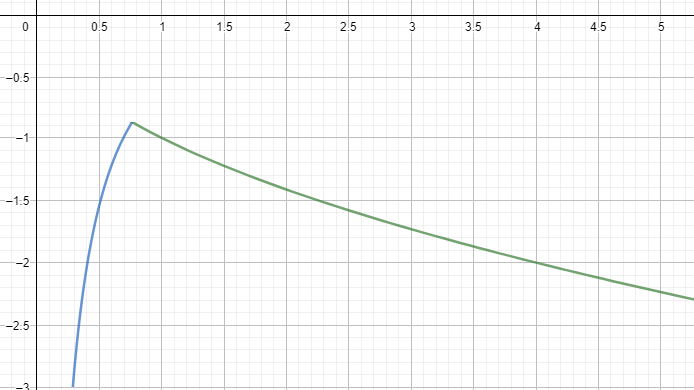
Ovviamente nel grafico l’effetto è stato volutamente esagerato, e nella realtà una linea con un falso contatto ha un HLog simile al seguente:
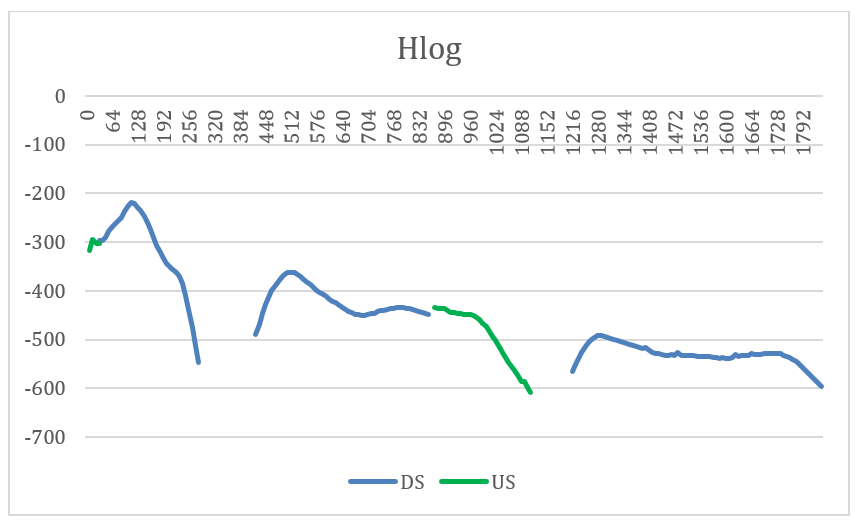
Verificare la presenza di derivazioni
In questo articolo non saranno approfondite le derivazioni, ma basti sapere che si ha una derivazione quando uno spezzone di cavo è collegato, in un qualunque punto, al cavo che parte dall’armadio e arriva alla presa del modem.
Questo spezzone di cavo “morto” provoca degli aumenti periodici di attenuazione, su frequenze diverse in base alla lunghezza della derivazione stessa.
Se ci sono più derivazioni, il loro effetto si sommerà su alcune frequenze specifiche.
Osservando un grafico HLog è possibile individuare la presenza di una derivazione: se invece di avere una linea sostanzialmente “lineare”, come quella dei primi due grafici (dove ogni punto ha un valore leggermente più grande del punto successivo), si hanno dei “picchi negativi” (ossia delle gobbe, o quello che visivamente può sembrare il profilo di una montagna capovolto), allora la linea ha delle derivazioni.
Per esempio:
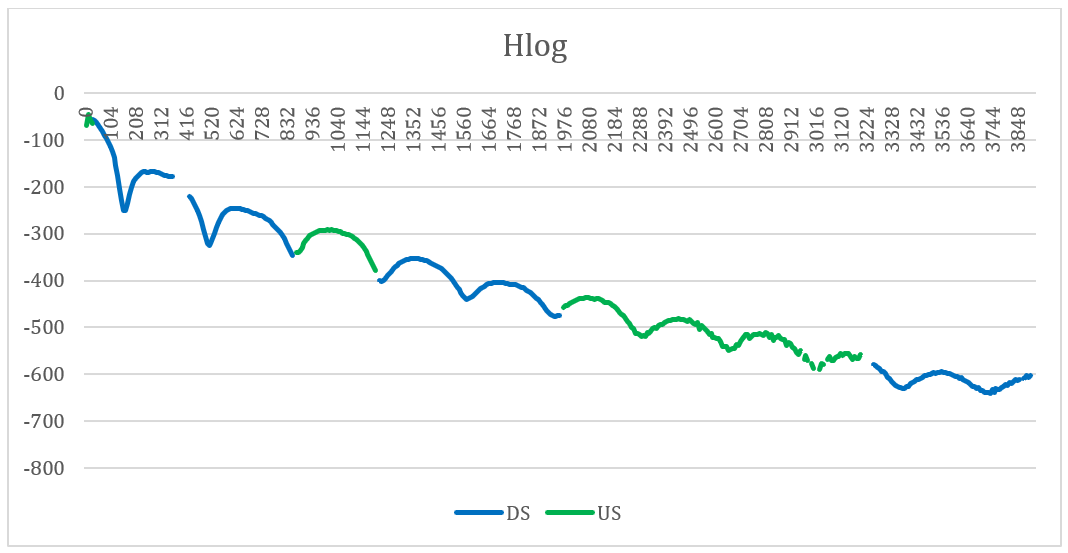
In questo caso è presente una derivazione, come si può vedere dalle varie “gobbe” presenti nel grafico.
Nel caso invece ci siano più derivazioni si avrà una situazione di questo tipo:
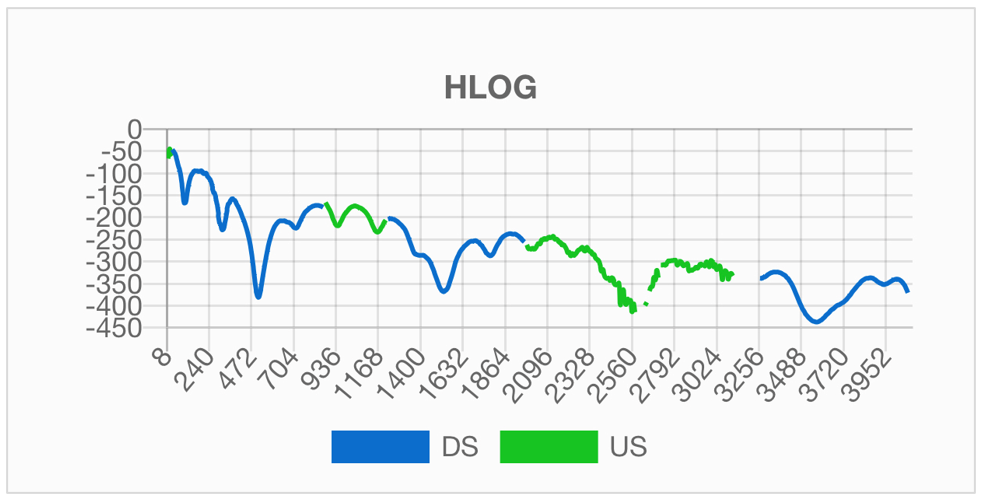
Si può osservare che in alcuni punti il picco di attenuazione è molto elevato e ha ampiezza maggiore rispetto ai picchi immediatamente successivi: in quei punti è presente una seconda derivazione.
Alcune note utili sulle derivazioni:
Minore è la lunghezza della derivazione, minore è il numero di portanti (frequenze) che vengono impattate, ma l’impatto su tali frequenze è elevato.
Più lunga è la derivazione, maggiore è il numero di frequenze impattate. Ma in questo caso l’impatto sarà minore.
In 17a la lunghezza minima della derivazione per essere impattante sulla linea è di poco inferiore a 3 metri.
In 35b la lunghezza minima della derivazione per essere impattante sulla linea è di poco inferiore a 1.5 metri.
Derivazioni più corte di tali valori non impatteranno la linea.
È meglio avere una derivazione lunga o corta? Entrambe, purché si rimanga agli estremi. Una derivazione estremamente lunga, sopra i 200 metri, ha un impatto marginale sulle prestazioni della linea. Per le derivazioni molto corte invece vale quanto scritto sopra.
Calcolare la lunghezza delle derivazioni
Il calcolo della lunghezza approssimativa degli stub è molto semplice (quantomeno finché di derivazione ce n’è soltanto una).
Innanzitutto è necessario prendere la frequenza del primo picco di attenuazione (il punto “più in basso”, o minimo locale, della prima gobba).
Nel caso in cui sul grafico non vi sia indicata la frequenza ma la portante è sufficiente moltiplicare il valore della portante corrispondente per lo spacing (4,3125 KHz).
Procediamo con un esempio e proviamo a calcolare la lunghezza della derivazione di questo grafico:

Il primo picco si ha alla portante 160.
Calcoliamo la rispettiva frequenza:
$$f = 160 \cdot 4,3125 kHz = 690 kHz$$Per calcolare la lunghezza in metri della derivazione, basterà applicare questa semplice formula:
$$Lunghezza = \frac{200\ 000}{f \cdot 4}$$Dove $f$ è la frequenza calcolata sopra.
Calcoliamo dunque la lunghezza della derivazione:
$$Lunghezza = \frac{200\ 000}{690 \cdot 4} \approx 72 m$$Nel caso ci siano più derivazioni la faccenda si complica per quanto riguarda il calcolo della lunghezza (non tanto a livello di calcoli, quanto nel riuscire a distinguere le varie derivazioni: non è sempre facile).
Riprendiamo come riferimento questo grafico HLog:

Possiamo ricavare:
- Prima derivazione: circa portante 100, quindi la lunghezza è di circa 115 metri.
- Seconda derivazione: circa portante 480, quindi la lunghezza è di circa 25 metri.
Il grafico QLN
Il QLN (o Quiet Line Noise) misura il rumore di fondo presente sulla linea, espresso in $\frac{dBm}{Hz}$ .
È uno strumento utile tra le altre cose a tentare di quantificare la diafonia presente su una linea. Tuttavia non bisogna pensare che la presenza di rumore implichi necessariamente diafonia (crosstalk), motivo per cui quando si valuta un QLN è più corretto parlare di rumore presente sulla linea e non di diafonia. Nella maggior parte dei casi resta comunque una buona approssimazione.
Il QLN è relativamente semplice da valutare: maggiore è il valore sull’asse delle ordinate maggiore è il rumore presente sulla linea alla data frequenza.
| Da | a | Significato |
|---|---|---|
| -145 | -130 | Rumore pressoché assente |
| -130 | -120 | Rumore basso |
| -120 | -110 | Rumore medio |
| -110 | -90 | Rumore elevato |